『计算机组成原理』数的表示及计算

@[toc]

三、数的表示及计算

1.定点数的表示

1.原码表示范围：

符号位和数据为 i 相对独立

N 位原码表示范围：

二进制形式：
[1111….11,01111…111]

整数：
$[-(2^{n-1}-1),2^{n-1}-1]$
共计：$2^n-1$

小数：
$[-(1-2^{-(n-1)}),1-2^{-(n-1)}]$
共计：$2^n-1$

因为 0 有两种表示，所以比 N 为能表示的状态少 1 种。

2.补码表示的范围

N 位补码表示范围

	-4	-2	-1	0	1	2	4
补码	1100	1110	1111	0000	0001	0010	0100
思考：
[1000]补 的真值是谁 ?

是-8，也就是说补码可以表示出比原码多一位的数，而且 0 的表示方法唯一。

考虑 N 为补码的表示形式：

	形式	真值 （整数）	真值（小数）
最大正数	011111…1111	$2^{n-1}-1	$1-2^{-(n-1)}$
最大负数	11..11111111	$-2^{n-1}$	$-(1-2^{-(n-1)})-2^{-(n-1)}=-1$

2.定点数运算

1.加减运算：

补码的加减法基本公式：

[A+B]补=[A]补+[B]补
[A-B]补=[A]补+[-B]补
优点：直接运算

溢出的判断：
双符号位法：两个符号位同时运算，双符号位不同则溢出，上溢和下溢。

2.移位运算

逻辑移位： 逻辑左移，逻辑右移

移出位移走，补位位补 0

eg：1010
左移：0100
右移：0101

循环移位：

小循环移位小循环左移，小循环右移
移出移入到补位位，同时移入到标记为 C 中
在数字最前和最后分别有一个 C 位，储存溢出位

eg：1010
左移：1  0101
右移：0101   0

大循环移位：大循环左移，大循环右移
移出位移入到 C 位，C 位移入到补位位

eg：0 1010
 左移：1 0100
 右移：0101 0

算数移位：

（1）保留数值的数学意义，左移相当于乘以 2，右移相当于除以 2
（2）存在溢出或精度丧失
原码：符号位不动，数值位逻辑左右移
补码：带着符号位一起移动
移出位移走。补位位：高位补符号位，地位补零。

溢出过半：

原码：符号位为 0 或 1，数值位最高位为 1
补码：符号位为 0，数值最高位为 1；符号位为 1，数值最高位为 0.

3.浮点数的表示

规则：
1）组成部分、顺序
2）每个组成部分位数
3）尾数和阶码表示形式：
尾数：定点小数
阶码：定点整数

一、IEEE754 标准
1.格式：
32 位（float）和 64 位（double）

2. IEEE 有关阶码的规定
（1）用修正过的移码表示
修正过的移码可以表示 0 和+-∞；

float：真值（e）=机器数的值（E）-128
double：真值（e）=机器数的值（E）-1024

（2）有关移码
$$e=E-2^{n-1}$$

（3）E 位全零或者全 1 的状态都不用

全0：表示数值0
全1：表示+-∞

所以正式的 IEEE754 标准：
$$e=E-(2^{n-1}-1)$$

3. IEEE 有关尾数的规定
（1）用修正过的原码表示尾数
（2）最高数值位必须为 1，并且省略。
==这样进一步提高了数据的精度。==
（3）什么是规格化的尾数（M）
$$|M|>=1/2=(0.1)_2$$

因为尾数最高的数值位为 1，并且省略。
E：阶码
S：符号位
M：尾数
float：$(-1)^s1.M2^{E-127}$
double:$(-1)^s1.M2^{E-1023}$

4. IEEE 与真值的相互转换
eg:Float 类型 413C0000H 的真值是多少:

$413C0000H
=(0100 0001 0011 1100 0000 0000 0000 0000)_2$

$S=0；M=0111；E=1000 0010$

$e=(-1)^s1.M2^{E-127}$
$=(-1)^01.011112^{130-127}$
$=(1011.11)_2$
$=11.75$

5. Float 类型的表示范围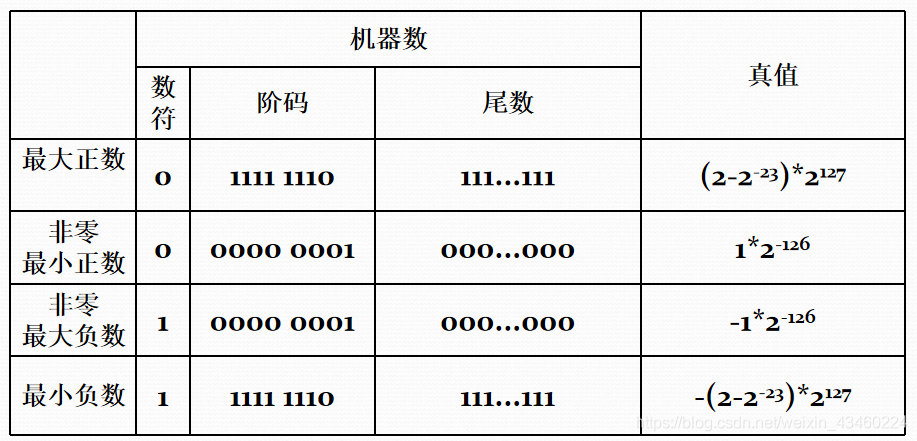

二、非 IEEE754 标准

1.有机组成部分

每部分可以用不同的编码表示，最常见的阶码和尾数都用补码表示。

2. 表示范围
（1）为什么要规格化？
==为了进一步提高数据精度==
（2）规格化的本质是什么？
$$|尾数|>=0.5$$

(3)这种本质的体现是什么？
尾数分别用原码和补码表示的时候规格化的尾数是什么形式的？
原码：数值最高位为 1
补码：1.0xxxxx 或者 0.1xxxxx 或者 1.1xxxxx

（4）IEEE754 标准如何做的规划化？
==尾数最高的数值位为 1，并且省略。==

设某浮点数阶码和尾数都用 4 位二进制补码表示。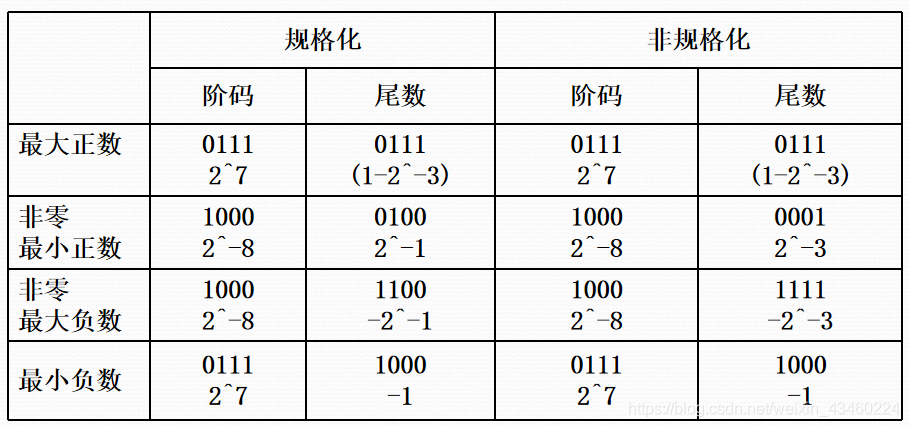

4.浮点数的运算

一、IEEE754 标准的加减运算
（1）0 操作数检查
（2）对阶：小阶向大阶对齐，尾数右移
（3）尾数加减：补码双符号位
（4）规格化： 左规；右规

左规：尾数+-不发生溢出，结果不是规格化，左规尾数不定，阶码-1，知道规格化为止；
右规：尾数+-发生溢出，带两个符号位右移移位，阶码+1

（5）舍入，阶码采用补码双符号位运算。==0 舍 1 入。==
（6）判断溢出
在溢出判断中，什么样的情况才算溢出？
==阶码溢出才叫溢出==
尾数溢出是否标志着结果的溢出？
==尾数溢出不表示结果的溢出==