『算法-ACM 竞赛-CodeForces』 1102A（思维题）

https://vjudge.net/problem/2135388/origin
Describe

You are given an integer sequence 1,2,…,n. You have to divide it into two sets A and B in such a way that each element belongs to exactly one set and |sum(A)−sum(B)| is minimum possible.

The value |x| is the absolute value of x and sum(S) is the sum of elements of the set S.

Input

The first line of the input contains one integer n (1≤n≤2⋅109).

Output

Print one integer — the minimum possible value of |sum(A)−sum(B)| if you divide the initial sequence 1,2,…,n into two sets A and B.

Examples

Input
3
Output
0
Input
5
Output
1
Input
6
Output
1
Note

Some (not all) possible answers to examples:

In the first example you can divide the initial sequence into sets A={1,2} and B={3} so the answer is 0.

In the second example you can divide the initial sequence into sets A={1,3,4} and B={2,5} so the answer is 1.

In the third example you can divide the initial sequence into sets A={1,4,5} and B={2,3,6} so the answer is 1.

这是一道思维题，刚拿到题的时候毛了，这是什么题，DP 背包容量为 1/2 值的和；不难发现这个题是个防爆零的送分题。
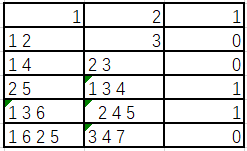
在表格中不难看出，当数字个数为偶数个时，要平分到两个组合，如果平分后个数为奇数肯定数组中间的两个值被分开，最小差值唯一，123456 分 1 / 6 分 2 / 5 分 3 /4，差值为 1； 当个数为奇数个时便有如下方法如果去掉最大之后，按照偶数分析。
AC 代码如下

#include<iostream>
#include<cstdio>
#include<map>
#include<cstring>
#include<cmath>
#include<vector>
#include<algorithm>
#include<map>
using namespace std;
#define mst(a,b) memset((a),(b),sizeof(a))
#define inf 0x3f3f3f3f
#define maxn 100
#define Abs(a) ((a)>0?(a):-(a))
int main()
{
    int n;
    cin>>n;
    if(n%2==1) {
        n=n-1;
        n/=2;
        if(n%2==1) cout<<'0'<<endl;
        else cout<<'1'<<endl;
        return 0;
    }
      else
      {
            n=n/2;
            if(n%2==0) cout<<'0'<<endl;
            else cout<<'1'<<endl;
            return 0;
      }
}