『算法-ACM 竞赛-数学-数论』HDU 1098 Ignatius’s puzzle （费马小定理+打表）

Ignatius’s puzzle

Problem Description
Ignatius is poor at math,he falls across a puzzle problem,so he has no choice but to appeal to Eddy. this problem describes that:f(x)=5x^13+13x^5+kax,input a nonegative integer k(k<10000),to find the minimal nonegative integer a,make the arbitrary integer x ,65|f(x)if
no exists that a,then print “no”.

Input
The input contains several test cases. Each test case consists of a nonegative integer k, More details in the Sample Input.

Output
The output contains a string “no”,if you can’t find a,or you should output a line contains the a.More details in the Sample Output.

Sample Input
11 100 9999

Sample Output
22 no 43

Author
eddy

Recommend
We have carefully selected several similar problems for you: 1071 1014 1052 1097 1082

题目大意：

给定一个 k，找到最小的 a 使得 f(x)=5x^13+13x^5+kax ，f(x)%65 永远等于 0

打表的话就很明显的看导规律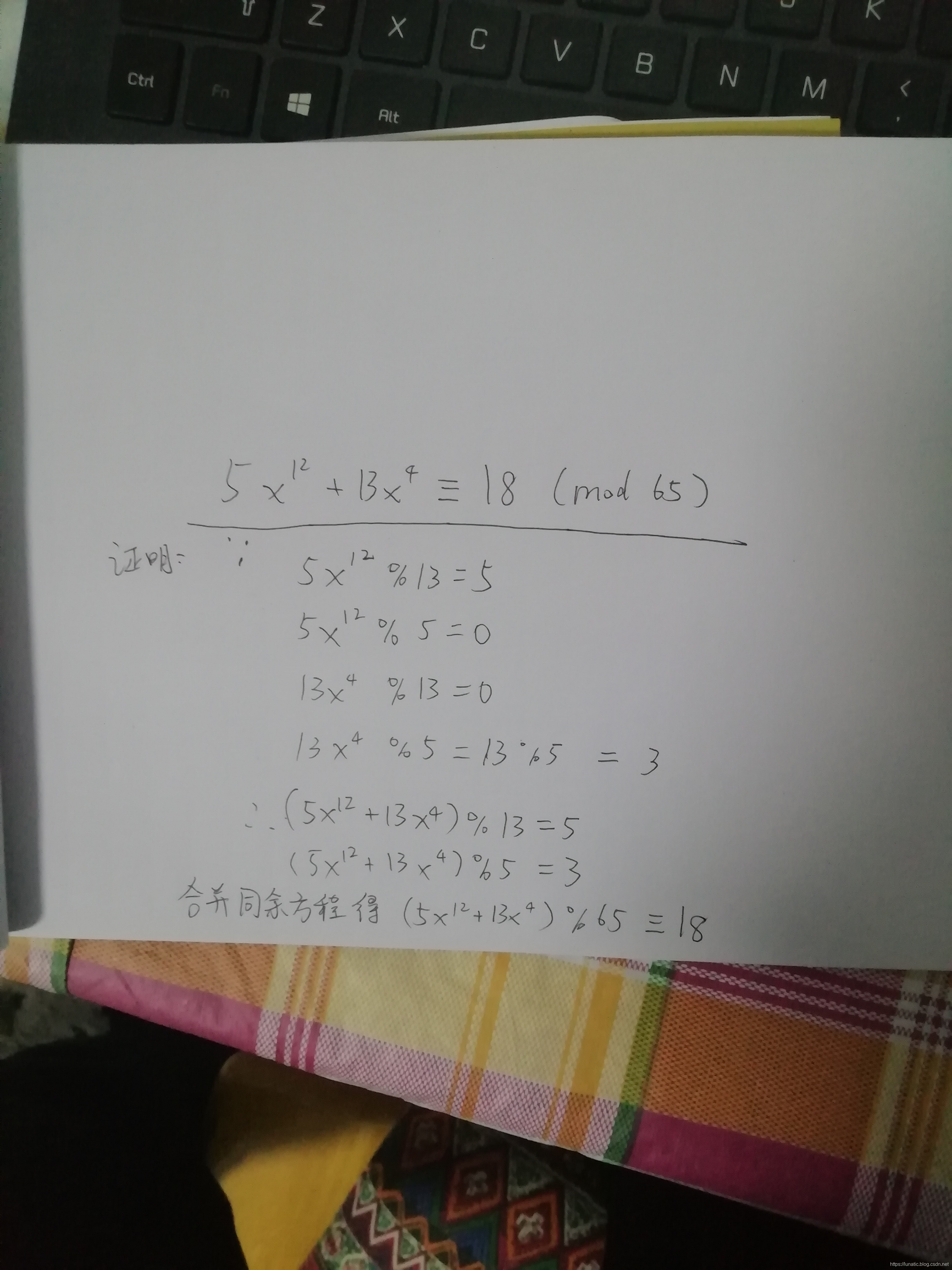
也可以用费马小定理证明

#include <iostream>
#include <cstdio>
using namespace std;
int gcd(int a, int b)
{
    if (a < b)
        return gcd(b, a);
    if (b == 0)
        return a;
    if ((a & 1) == 0 && (b & 1) == 0)
        return 2 * gcd(a >> 1, b >> 1); //a and b are even
    if ((a & 1) == 0)
        return gcd(a >> 1, b); // only a is  even
    if ((b & 1) == 0)
        return gcd(a, b >> 1);              // only b is  even
    return gcd((a + b) >> 1, (a - b) >> 1); // a and b are odd
}
int main()
{
    int k;
    while (scanf("%d", &k) != EOF)
    {
        if (18 % gcd(k, 65) == 0)
        {
            for (int a = 0;; a++)
            {
                if ((18 + k * a) % 65 == 0)
                {
                    printf("%d\n", a);
                    break;
                }
            }
        }
        else
            printf("no\n");
    }
    return 0;
}