『算法-ACM竞赛-数学-数论』费马小定理+求逆元
『算法-ACM 竞赛-数学-数论』费马小定理+求逆元
1.费马小定理: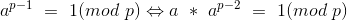
(此处的 p 为素数)
证明:
费马小定理求逆元
如果 p 为小素数我们选择直接暴力,时间复杂度为:
1 | |
如果 p 为大素数,我们可以用快速幂求解,时间复杂度为:
1 | |
『算法-ACM竞赛-数学-数论』费马小定理+求逆元
https://chiamzhang.github.io/2024/06/29/『算法-ACM竞赛-数学-数论』费马小定理+求逆元/
1.费马小定理: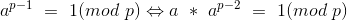
(此处的 p 为素数)
证明:
费马小定理求逆元
如果 p 为小素数我们选择直接暴力,时间复杂度为:
1 | |
如果 p 为大素数,我们可以用快速幂求解,时间复杂度为:
1 | |