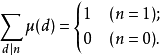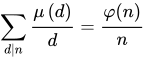『算法-ACM 竞赛-数学-数论』莫比乌斯函数

定义：
默比乌斯函数或缪比乌斯函数是指以下的函数 ：
$μ(n)= \left{
\begin{aligned}
1& \ \ \ \text{若n=1};\
(-1)^k& \ \ \ 若n无平方因子数，且n=p_1*p_2….*p_k ;\
0& \ \ \ 若n有平方因子数
\end{aligned}
\right.$

性质：
我们之前就提到过，莫比乌斯是积性函数，必然满足积性函数的性质
积性函数
性质 1:

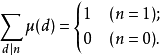
性质 2：

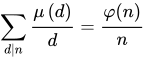
莫比乌斯函数值求法：
1.单个函数值：

#include <iostream>

using namespace std;
typedef long long ll;
//计算a是否可以mod b
int MOD(int a,int b)
{
    return a-a/b*b;
}

//计算莫比乌斯函数
//如果一个数包含平方因子，那么miu(n)=0
//如果哟个数不包含平方因子，且有k个不同的质因子，那么miu(n)=(-1)^k

int miu(int n)
{
    int cnt,k=0;
    for(int i=2;i*i<n;i++)
    {
        if(MOD(n,i))
        {
            continue;
        }
        cnt=0;
        k++;
        while(MOD(n,i)==0)
        {
            n/=i;
            cnt++;
        }
        if(cnt>=2)
        {
            return 0;
        }

    }
    if(n!=1)
    {
        k++;
    }
    return MOD(k,2)?-1:1;
}

int main()
{
    ll n;
    cin>>n;
    cout<<miu(n)<<endl;
    return 0;
}

2.线性筛：

/*
 *  莫比乌斯反演公式
 *  线性筛法求解积性函数（莫比乌斯函数）
 */
const int MAXN = 1000000;
bool check[MAXN + 10];
int prime[MAXN + 10];
int mu[MAXN + 10];

void Moblus()
{
    memset(check, false, sizeof(check));
    mu[1] = 1;
    int tot = 0;
    for (int i = 2; i <= MAXN; i++)
    {
        if (!check[i])
        {
            prime[tot++] = i;
            mu[i] = -1;
        }
        for (int j = 0; j < tot; j++)
        {
            if (i * prime[j] > MAXN)
            {
                break;
            }
            check[i * prime[j]] = true;
            if (i % prime[j] == 0)
            {
                mu[i * prime[j]] = 0;
                break;
            }
            else
            {
                mu[i * prime[j]] = -mu[i];
            }
        }
    }
}