『算法-ACM 竞赛-数学-数论』积性函数（初步）

一、定义
积性函数指对于所有互质的整数 a 和 b 有性质 f(ab)=f(a)f(b)的数论函数。
二、常见的积性函数
φ(n) －欧拉函数
μ(n) －莫比乌斯函数，关于非平方数的质因子数目
gcd(n,k) －最大公因子，当 k 固定的情况
d(n) －n 的正因子数目
σ(n) －n 的所有正因子之和
ε(n) －定义为：若 n = 1，ε(n)=1；若 n > 1，ε(n)=0。别称为“对于狄利克雷卷积的乘法单位”（完全积性）
λ(n) －刘维尔函数，关于能整除 n 的质因子的数目
性质 1.若将 n 表示成质因子分解式

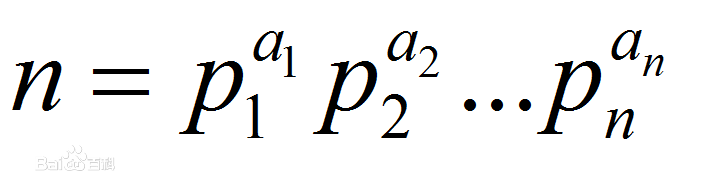
则有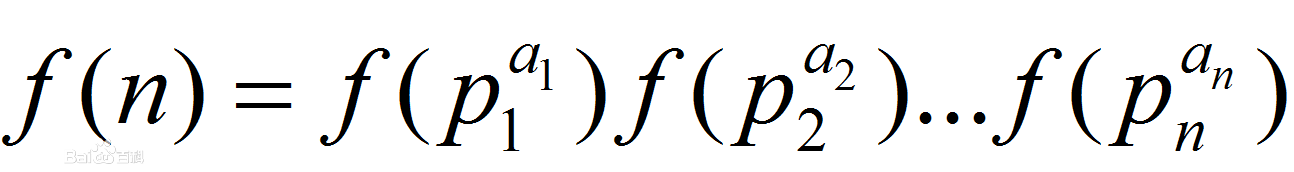
2.若 f 为积性函数且有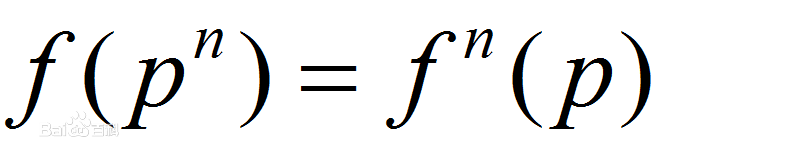

则 f 为完全积性函数。

特点：
积性函数都可以用线筛处理，就是说复杂度是 O(n)。