『算法-ACM 竞赛-数学-数论』中国剩余定理+扩展中国剩余定理（孙子定理）

中国剩余定理

问题

求解同余方程组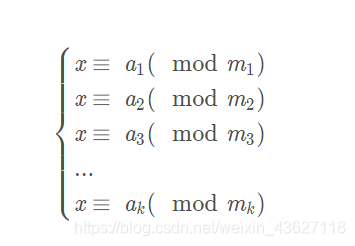

其中$m_1,m_2,m_3…m_k$为两两互质的整数
求 x 的最小非负整数解

定理
令$M=\prod_{i=1}^km_i$，即 M 是所有 $m_i$的最小公倍数
$t_i$为同余方程 $M_t/m_i ≡ 1(mod\ m_i )$的最小非负整数解
则有一个解为$x=\sum_{i=1}^ka_i\frac{M}{m_i}t_i$
通解为$x+i*M(i\in Z)$
特别的，最小非负整数解为(x%M+M)%M
证明

代码实现
同余式的求解可以用扩展欧几里得

void exgcd(int a,int b,int &x,int &y)
{
    if(b==0){ x=1; y=0; return;}
    exgcd(b,a%b,x,y);
    int tp=x;
    x=y; y=tp-a/b*y;
}

int china()
{
    int ans=0,lcm=1,x,y;
    for(int i=1;i<=k;++i) lcm*=b[i];
    for(int i=1;i<=k;++i)
    {
        int tp=lcm/b[i];
        exgcd(tp,b[i],x,y);
        x=(x%b[i]+b[i])%b[i];//x要为最小非负整数解
        ans=(ans+tp*x*a[i])%lcm;
    }
    return (ans+lcm)%lcm;
}

扩展中国剩余定理

求解同余方程组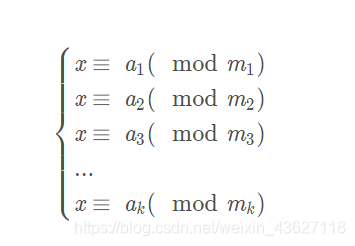

其中$m_1,m_2,m_3…m_k$不一定为两两互质的整数
求 x 的最小非负整数解
求解：
求解
假设已经求出前 k-1 个方程组成的同余方程组的一个解为 x
且有$M=\prod_{i-1}^{k-1}m_i$
则前 k-1 个方程的方程组通解为 x+i∗M(i∈Z)x+i*M(i\in Z)x+i∗M(i∈Z)

那么对于加入第 k 个方程后的方程组
我们就是要求一个正整数 t，使得
$x+t∗M≡a_k(mod \ m_k)$

转化一下上述式子得
$t∗M≡a_k−x(mod\ m_k )$

对于这个式子我们已经可以通过扩展欧几里得求解 t
若该同余式无解，则整个方程组无解
若有，则前 k 个同余式组成的方程组的一个解解为$x_k=x+t*M$

所以整个算法的思路就是求解 k 次扩展欧几里得

#include<iostream>
using namespace std;
#define LL long long
LL mi[1100],ai[1100];//mi为要模的数,ai为余数。
LL gcd(LL a, LL b)
{
    return b == 0 ? a : gcd(b, a%b);
}
void exgcd(LL a, LL b, LL &d, LL &x, LL &y)
{
    if(!b)
    {
        d = a, x = 1, y = 0;
    }
    else
    {
        exgcd(b, a%b, d, y, x);
        y -= x * (a / b);
    }
}
LL CRT(LL l, LL r, LL *mi, LL *ai)
{
    LL lcm = 1;
    for(LL i = l; i <= r; i++)
        lcm = lcm / gcd(lcm, mi[i]) * mi[i];
    for(LL i = l+1; i <= r; i++)
    {
        LL A = mi[l], B = mi[i], d, x, y, c = ai[i] - ai[l];
        exgcd(A, B, d, x, y);
        if(c % d)
            return -1;
        LL mod = mi[i] / d;
        LL k = ((x * c / d) % mod + mod) % mod;
        ai[l] = mi[l] * k + ai[l];
        mi[l] = mi[l] * mi[i] / d;
    }
    /*if(ai[l] == 0)
        return lcm;*/ //保证结果为正整数
    return ai[l];
}
int main()
{
    LL t,n,i,aa;
    while(cin>>n>>aa)
    {
		if(n==0) break;
        for(i=1; i<=n; i++){
            cin>>mi[i];
			ai[i]=mi[i]-aa;
		}
        cout<<CRT(1ll,n,mi,ai)<<endl;
    }
    return 0;
}