『算法-ACM 竞赛-数学-数论』 组合数+卢卡斯定理+扩展卢卡斯定理 (3)

**欧拉函数定义
对正整数 n，欧拉函数是少于或等于 n 的数中与 n 互质的数的数目。例如 euler(8)=4，因为 1,3,5,7 均和 8 互质。

Euler 函数表达通式：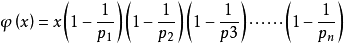

其中 p1,p2……pn 为 x 的所有素因数，x 是不为 0 的整数。euler(1)=1（唯一和 1 互质的数就是 1 本身）。

欧拉公式的延伸：
一个数的所有质因子之和是 Euler(n)*n/2。

欧拉函数的相关性质： 3. 欧拉函数性质

$(1)欧拉函数为积性函数。\(对于数论函数 f(n) 不恒等于0，当 (m,n) = 1 时，满足 f(mn) = f(m)f(n) ，则称 f(n) 为积性函数)\ \qquadφ(mn) = φ(m)φ(n)，(m,n) = 1\(2)若 (m,n) = d，则φ(mn) = dφ(m)φ(n)/φ(d)\ (3)若m、n满足m|n，则φ(mn) = mφ(n)\
(4)若m、n满足m|n，则
φ(m)|φ(n)
(5)对于质数p，其欧拉函数公式为
φ(p) = p-1\
(6)对于质数p，pk的欧拉函数公式为
φ(pk) = (p-1)pk-1\
(7)小于等于n且整除n的所有正整数的欧拉函数值之和等于n，即
n = Σd|nφ(d)\
(8)欧拉定理：若(a,m) = 1，则 aφ(m) ≡ 1 (mod m)。\
(9)扩展欧拉定理\
\qquad ax ≡ ax mod φ(m) (mod m)，(a,m) = 1\
\qquad或 ax ≡ ax (mod m)，(a,m) ≠ 1且x < φ(m)\
\qquad或 ax ≡ ax mod φ(m) + φ(m) (mod m)，(a,m) ≠ 1且x ≥ φ(m)$
求欧拉函数的值：

//求欧拉函数板子
//根号n求欧拉函数 注意是 i*i<=x
//适用于需要求得欧拉函数少的时候
int getphi(int x)
{
    int tmp=x;
    for(int i=2;i*i<=x;i++){
        if(x%i==0){
            while(x%i==0) x/=i;
            tmp/=i;tmp*=(i-1);
        }
    }
    if(x>1) tmp/=x,tmp*=(x-1);
    return tmp;
}

typedef long long ll;
bool ok[maxn];
int prime[maxn],phi[maxn],cnt;
void sieve()
{
        phi[1]=1;
	for(ll i=2;i<maxn;++i)
	{
		if(!ok[i])
		{
			prime[cnt++]=i;
			phi[i]=i-1;
		}
		for(int j=0;j<cnt;++j)
		{
			if(i*prime[j]>=maxn)break;
			ok[i*prime[j]]=1;
			if(i%prime[j]==0)
			{
				phi[i*prime[j]]=phi[i]*prime[j];//prime[j]是i的因子 prime[j]的素因子项包含在i的素因子项里
				break;
			}
			else phi[i*prime[j]]=phi[i]*(prime[j]-1);//prime[j]与i互质 phi[i*prime[j]=phi[i]*phi[prime[j]]
		}
	}
}

解释：