『算法-ACM竞赛-数学-数论』 组合数+卢卡斯定理+扩展卢卡斯定理 (1)

『算法-ACM 竞赛-数学-数论』 组合数+卢卡斯定理+扩展卢卡斯定理 (1)

组合数：
在 N 个数中选取 M 个数，问选的方式有几种？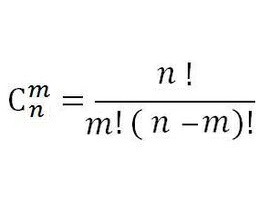
在这里插入图片描述
直接递归暴力简单

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
#include<cstdio>
const int N = 2000 + 5;
const int MOD = (int)1e9 + 7;
int comb[N][N];//comb[n][m]就是C(n,m)
void init(){
    for(int i = 0; i < N; i ++){
        comb[i][0] = comb[i][i] = 1;
        for(int j = 1; j < i; j ++){
            comb[i][j] = comb[i-1][j] + comb[i-1][j-1];
            comb[i][j] %= MOD;
        }
    }
}
int main(){
    init();
}

卢卡斯定理：
求$C_m^nmodp$
设$m={a_0}^{p_0}+{a_1}^{p_1}+\cdots+{a_k}^{p_k}$
设$n={b_0}^{p_0}+{b_1}^{p_1}+\cdots+{b_k}^{p_k}$
则$C_m^n\equiv\prod{C_{a_i}^{b_i}}(mod~p)$

证明我就不打了，百度百科上有，数学符号太多了~ _ ~
前置知识： 1.欧几里得或者费马小定理求逆元 2.快速幂
实现代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
#include<iostream>
using namespace std;
typedef long long LL;
const LL N=1e5+2;
LL a[N];
void init(LL p)
{
	a[1]=1;
	for(int i=2;i<=p;++i)a[i]=a[i-1]*i%p;
}
void exgcd(LL a,LL b,LL &x,LL &y)
{
	if(!b){
		x=1;
		y=0;
		return;
	}
	exgcd(b,a%b,y,x);
	y-=a/b*x;
}
LL ksm(LL x,LL n,LL mod)
{
	LL ans=1;
	while(n){
		if(n&1)ans=ans*x%mod;
		n>>=1;
		x=x*x%mod;
	}
	return ans;
}
LL C(LL n,LL m,LL p)
{
	if(n==m||m==0)return 1;
	if(n<m)return 0;
	if(m*2>n)m=n-m;						  /*C(n,m)=c(n,n-m)*/
	return a[n]*ksm(a[m]*a[n-m],p-2,p)%p; /*求(a[m]*a[n-m])在(mod p)意义下的乘法逆元*/
										  /*拓展欧几里得与费马小定理均可*/
	/*LL x,y;
	exgcd(a[m]*a[n-m],p,x,y);
	return (a[n]*x%p+p)%p;*/
}
LL lucas(LL n,LL m,LL p)
{
	if(!m)return 1;
	return lucas(n/p,m/p,p)*C(n%p,m%p,p)%p;
}
int main()
{
	ios::sync_with_stdio(false);
	LL T,n,m,p;
	cin>>T;
	while(T--){
		cin>>n>>m>>p;
		init(p);
		cout<<lucas(n+m,m,p)<<endl;
	}
	return 0;
}

为了快，放了一个数组，限制了 P 的大小，然后再发一个没有限制的卢卡斯。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
#define MOD 1000000007
typedef long long LL;

LL quickPower(LL a, LL b)
{
    LL ans = 1;
    a %= MOD;
    while (b)
    {
        if (b & 1)
        {
            ans = ans * a % MOD;
        }
        b >>= 1;
        a = a * a % MOD;
    }
    return ans;
}

LL c(LL n, LL m)
{
    if (m > n)
    {
        return 0;
    }
    LL ans = 1;
    for (int i = 1; i <= m; i++)
    {
        LL a = (n + i - m) % MOD;
        LL b = i % MOD;
        ans = ans * (a * quickPower(b, MOD - 2) % MOD) % MOD;
    }
    return ans;
}

LL lucas(LL n, LL m)
{
    if (m == 0)
    {
        return 1;
    }
    return c(n % MOD, m % MOD) * lucas(n / MOD, m / MOD) % MOD;
}

int main(int argc, const char * argv[])
{
    LL n, m;
    while (~scanf("%lld %lld", &n, &m))
    {
        LL max, min;
        max = n + m - 3;
        min = m - 1;
        printf("%lld\n", lucas(max - 1, min - 1));
    }
    return 0;
}

ExLucas 扩展卢卡斯定理：
求解$C_{n}^{m}% P$,其中 m,n 较大，P 较小且不一定为素数
转化为 CRT（中国剩余定理）
好像这也不是什么定理，只是一个计算方法
$计算C_{n}^{m}% P，其中p=p1^{q1}×p2^{q2}×⋯pk^{qk}时，我们可以先求出C_m^nmod{p_i}^{q_i}，然后用CRT合并。\
那么怎么计算C_m^nmod{p_i}^{q_i}呢？\
C_m^n=\frac{m!}{n!(m-n)!}，我们只需要算出m!,n!^{−1},(m−n)!^{−1} ，然后乘在一起。\
注：n! 可能在模{p_i}^{q_i}的意义下没有逆元啊，那这就是错的了\
其实这里求得不是逆元（可能没有逆元），求出来的是a\times {p_i}^b(gcd(a,p)=1)，\前面的aa用逆元，后面的次数加加减减一下就好了\
问题转换成求n!modp^q\
例如n=19,p=3,q=2n=19,p=3,q=2：$
参考
$19!\
=1×2×3×⋯×19\
=(1×2×4×5×7×8⋯×16×17×19)×(3×6×9×12×15×18)\
=(1×2×4×5×7×8⋯×16×17)×19×36×(1×2×3×4×5×6)\
=(1×2×4×5×7×8)2×19×36×(1×2×3×4×5×6)$

上面这个式子分为四部分：
$第一部分：(1×2×4×5×7×8)2(1×2×4×5×7×8)2。这部分的数不超过pqpq个，可以暴力算\
第二部分：1919。这部分的数不超过pqpq个，可以暴力算\
第三部分：3636。这个在最后处理时求出m!,n!,(m−n)!m!,n!,(m−n)!\ \qquad\ \ \ \ \ \ \ \ \ \ \ \ 分别有多少个pp（设为x,y,zx,y,z），则答案要乘上px−y−zpx−y−z\
第四部分：1×2×3×4×5×61×2×3×4×5×6。\
\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 这个是⌊np⌋!⌊np⌋!，可以递归处理$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const LL N=1e5+9;
LL A[N],M[N];
LL ksm(LL x,LL n,LL mod)
{
	LL ans=1;
	while(n){
		if(n&1)ans=ans*x%mod;
		n>>=1,x=x*x%mod;
	}
	return ans;
}
void exgcd(LL a,LL b,LL &x,LL &y)
{
	if(!b)x=1,y=0;
	else exgcd(b,a%b,y,x),y-=a/b*x;
}
LL inv(LL a,LL p)
{
	LL x,y;
	exgcd(a,p,x,y);
	return (x+p)%p?x:x+p;
}
LL get(LL n,LL pi,LL p)									/*求(与pi互素后的n!)%M[i]*/
{
	if(!n)return 1;
	LL ans=1;
	if(n/p){											/*判断有无循环节 */
		for(LL i=2;i<=p;++i)if(i%pi)ans=ans*i%p;
		ans=ksm(ans,n/p,p);
	}
	for(LL i=2;i<=n%p;++i)if(i%pi)ans=ans*i%p;			/*循环节剩余部分*/
	return ans*get(n/pi,pi,p)%p;
}
LL exlucas(LL n,LL m,LL pi,LL p)						/*求A[i]*/
{
	LL nn=get(n,pi,p);									/*求(与pi互素后的n)%M[i]*/
	LL mm=get(m,pi,p);									/*求(m!与pi互素后的m!)%M[i]*/
	LL nm=get(n-m,pi,p);								/*求(与pi互素后的(n-m)!)%M[i]*/
	LL k=0;												/*含质因数pi的数量*/
	for(LL i=n;i;i/=pi)k+=i/pi;
	for(LL i=m;i;i/=pi)k-=i/pi;
	for(LL i=n-m;i;i/=pi)k-=i/pi;
	return nn*inv(mm,p)*inv(nm,p)*ksm(pi,k,p)%p;
}
LL crt(LL len,LL Lcm)
{
	LL ans=0;
	for(LL i=1;i<=len;++i){
		LL Mi=Lcm/M[i];
		ans=((ans+A[i]*inv(Mi,M[i])*Mi)%Lcm+Lcm)%Lcm;
	}
	return ans;
}
int main()
{
	ios::sync_with_stdio(false);
	LL n,m,P,num;
	while(cin>>n>>m>>P){
		if(n<m){
			cout<<0<<endl;
			continue;
		}
		num=0;
		memset(A,0,sizeof(A));
		memset(M,0,sizeof(M));
		for(LL x=P,i=2;i<=P;++i)
			if(x%i==0){
				M[++num]=1;
				while(x%i==0){
					M[num]*=i;
					x/=i;
				}
				A[num]=exlucas(n,m,i,M[num])%P;
			}
		cout<<crt(num,P)<<endl;
	}
	return 0;
}
算法 > ACM竞赛 > 数学 > 数论
『算法-ACM竞赛-数学-数论』 组合数+卢卡斯定理+扩展卢卡斯定理 (1)
https://chiamzhang.github.io/2024/06/29/『算法-ACM竞赛-数学-数论』 组合数+卢卡斯定理+扩展卢卡斯定理 (1)/
Author
Chiam
Posted on
June 29, 2024
Licensed under