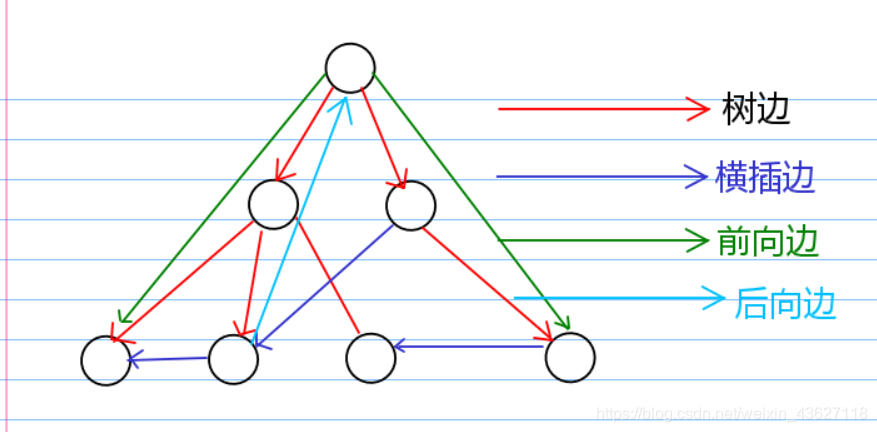
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
| #include<iostream>
#include<queue>
#include<algorithm>
#include<set>
#include<cmath>
#include<vector>
#include<map>
#include<stack>
#include<bitset>
#include<cstdio>
#include<cstring>
#define cini(n) scanf("%d",&n)
#define cinl(n) scanf("%lld",&n)
#define cinc(n) scanf("%c",&n)
#define cins(s) scanf("%s",s)
#define coui(n) printf("%d",n)
#define couc(n) printf("%c",n)
#define coul(n) printf("%lld",n)
#define debug(n) printf("%d_________________________________\n",n);
#define speed ios_base::sync_with_stdio(0)
#define file freopen("input.txt","r",stdin);freopen("output.txt","w",stdout)
#define rep(i,a,n) for(int i=a;i<=n;i++)
#define per(i,n,a) for(int i=n;i>=a;i--)
#define Swap(a,b) a^=b^=a^=b
#define Max(a,b) (a>b?a:b)
#define Min(a,b) a<b?a:b
#define mem(n,x) memset(n,x,sizeof(n))
#define mp(a,b) make_pair(a,b)
#define pb(n) push_back(n)
#define dis(a,b,c,d) ((double)sqrt((a-c)*(a-c)+(b-d)*(b-d)))
#define INF 0x3f3f3f3f
#define esp 1e-9
#define PI acos(-1)
using namespace std;
#define maxn 1020
#define INF 0x3f3f3f3f
using namespace std;
int pre[101],post[101],edge[101][101],parent[101];
int tag;
void dfs_tag(int cur,int n){
pre[cur]=++tag;
for(int i=0;i<n;i++){
if(edge[cur][i]==1){
if(pre[i]==0){
parent[i]=cur;
edge[cur][i]=-1;
dfs_tag(i,n);
}else{
if(post[i]==0){edge[cur][i]=-2;}
else if(pre[i]>pre[cur]){
edge[cur][i]=-3;
}else{
edge[cur][i]=-4;
}
}
}
}
post[cur]=++tag;
}
void dfs(int n){
memset(pre,0,sizeof(pre));
memset(post,0,sizeof(post));
memset(parent,-1,sizeof(parent));
for (int i = 0; i < n; ++i)
{
if(parent[i]==-1)
dfs_tag(i,n);
}
}
int main(){
int n,m;
int u,v;
int cases;
tag=0;
cin>>m>>n;
for (int i = 0; i < m; ++i)
{
cin>>u>>v;
edge[u][v]=1;
}
dfs(n);
cin>>cases;
while(cases--){
cin>>u>>v;
switch(edge[u][v]){
case -1:
printf("edge (%d,%d) is Tree Edge\n",u,v);
break;
case -2:
printf("edge (%d,%d) is Back Edge\n",u,v);
break;
case -3:
printf("edge (%d,%d) is Down Edge\n",u,v);
break;
case -4:
printf("edge (%d,%d) is Cross Edge\n",u,v);
break;
}
}
}
|