『算法-ACM 竞赛-图论』图的割点、桥和双连通分支的基本概念

点连通度与边连通度

回到正题，首先介绍下什么是图的边连通度和点连通度。一般来说，点连通度是指对应一个图 G，对于所有点集 U 属于 V（G），也就是 V（G）的子集中，使得 G-U 要么是一个非连通图，要么就是一个平凡图（即仅包含一个独立点的图），其中最小的集合 U 的大小就是图 G 的点连通度，有时候也直接称为图的连通度。通俗点说，就是一个图 G 最少要去掉多少个点会变成非连通图或者平凡图。当然对于一个完全图来说 Kn 来说，它的连通度就是 n-1。
同理，边连通度就是对于一个非平凡图 G，至少去掉多少条边才能使得该图变成非连通图。我们的问题就是，对于任意一个图，如何求该图的连通度以及边连通度？这跟最大流问题有什么联系？
简单起见，我们先说如何求一个图的边连通度 lamda(G)。（基于无向图考虑）
对于图 G，设 u，v 是图 G 上的两个顶点，定义 r（u，v）为删除最少的边，使得 u 到 v 之间没有通路。将图 G 转换成一个流网络 H，u 为源点，v 是汇点，边容量均为 1，那么显然 r（u，v）就是流网络的最小割，根据（二）里的介绍，其等于流网络的最大流。
但是，目前为止我们还没解决完问题，因为显然我们要求的边连通度 lamda（G）是所有的点对<u,v>对应的 r（u，v）中最小的那个值。这样的话我们就必须遍历所有的点对，遍历的的复杂度为 O（n*n）。这显然代价太高，而事实上，我们也不必遍历所有点对。

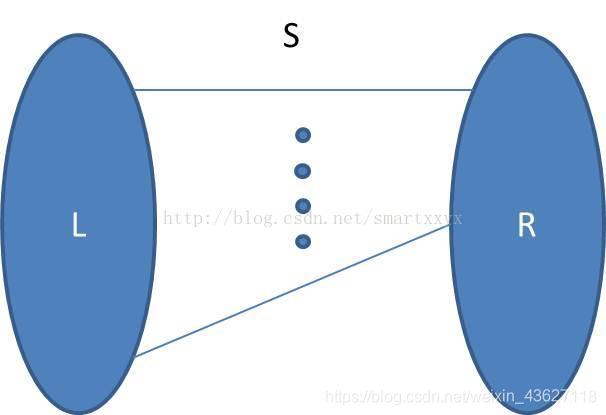
如图所示，设 S 为图 G 的最小割集，那么 lamda（G）=|S|。设在取任意一个点 u，若 u 在 L 内，那么必然至少存在一个点 v，使得 r（u，v）=|S|（v 是在 R 内时即成立）。所以，我们只需要任取一个点 u，计算 u 和其他点的 r（u，v），取最小者，必然是等于最小割集，即边连通度。

双连通图、割点与桥

点连通度与边连通度：
在一个无向连通图中，如果有一个顶点集合 v，删除顶点集合 v，以及与 v 中顶点相连 （至少有一端在 v 中）的所有边后，原图不连通，就称这个点集 v 为割点集合。
一个图的点连通度的定义为：最小割点集合中的顶点数。
类似的，如果有一个边集合，删除这个边集合以后，原图不连通，就称这个点集为割边 集合。
一个图的边连通度的定义为：最小割边集合中的边数。

双连通图、割点与桥：
如果一个无向连通图的点连通度大于 1，则称该图是点双连通的 (point biconnected)，简 称双连通或重连通。一个图有割点，当且仅当这个图的点连通度为 1，则割点集合的唯一元素被称为割点(cut point)，又叫关节点(articulationpoint)。一个图可能有多个割点。
如果一个无向连通图的边连通度大于 1，则称该图是边双连通的 (edge biconnected)，简 称双连通或重连通。一个图有桥，当且仅当这个图的边连通度为 ，则割边集合的唯一元素 被称为桥(bridge)，又叫关节边(articulationedge)。一个图可能有多个桥。
可以看出，点双连通与边双连通都可以简称为双连通，它们之间是有着某种联系的，下 文中提到的双连通，均既可指点双连通，又可指边双连通。（但这并不意味着它们等价)。

双连通分量（分支）
在图 G 的所有子图 G’中，如果 G’是双连通的，则称 G’为双连通 子图。如果一个双连通子图 G’它不是任何一个双连通子图的真子集，则 为极大双连通子 图。双连通分量(biconnectedcomponent)，或重连通分量，就是图的极大双连通子图。特殊的，点双连通分量又叫做块。

Tarjan 算法
与有向图求强连通分量的 Tarjan 算法类似，只需通过求 dfn 值与 low 值来得出割点与桥。
对图深度优先搜索(DFS)，定义 dfn(u)为 u 在搜索树 （以下简称为树）中被遍历到的次序号。定义 low(u)为 u 或 u 子树中的结点经过最多一条后向边能追溯到的最早的树中结点次序号(注意：与 DAG 不同的是，这里的后向边不包括与搜索树中父亲的连边)。
根据定义，则有：
low(u)=Min{}dfn(u)dfn(v)(u,v)为后向边（返祖边）（一定注意不包括与父节点的连边）low(v)(u,v)为树枝边 low(u)=Min{dfn(u)dfn(v)(u,v)为后向边（返祖边）（一定注意不包括与父节点的连边）low(v)(u,v)为树枝边}
一个顶点 u 是割点，当且仅当满足 (1)或(2)：
(1)u 为树根，且 u 有多于一个子树。因为无向图 DFS 搜索树中不存在横叉边，所以若有多个子树，这些子树间不会有边相连。
(2)u 不为树根，且满足存在(u,v)为树枝边 （即 为 在搜索树中的父亲），并使得 DFN(u)<=Low(v).（因为删去 后 以及 的子树不能到达 的其他子树以及祖先）。

实现时，因为有重边的问题，所以需要将一条无向边拆为两条编号一样的有向边，用邻 接表进行存储。在判断 是否为后向边时要注意是树枝边的反向边还是新的一条反向边。

求双连通分量
下面要分开讨论点双连通分量与边双连通分量的求法。

对于点双连通分量，实际上在求割点的过程中就能顺便把每个点双连通分支求量。建立 一个栈，存储当前双连通分量，在搜索图时，每找到一条树枝边或后向边（非横叉边），就 把这条边加入栈中。如果遇到某时满足 DFN(u)<=Low(v) 说明 u 是一个割点，同时把边从栈 顶一个个取出，直到遇到了边(u,v) ，取出的这些边与其相连的点，组成一个点双连通分量。割点可以属于多个点双连通分量，其余点和每条边只属于且属于一个点双连通分量。
（这里选择储存边而不是储存点是因为一个割点可以属于多个点双连通分量）

对于边双连通分量，求法更为简单。只需在求出所有的桥以后，把桥边删除，原图变成了多个连通块，则每个连通块就是一个边双连通分量。桥不属于任何一个边双连通分量，其 余的边和每个顶点都属于且只属于一个边双连通分量。可以用并查集实现。 （一定注意考虑重边的可能性）

一个有桥的连通图，如何把它通过加边变成边双连通图？

方法为首先求出所有的桥，然 后删除这些桥边，剩下的每个连通块都是一个双连通子图。把每个双连通子图收缩为一个顶点，再把桥边加回来，最后的这个图一定是一棵树，边连通度为 1。
统计出树中度为 1 的节点的个数，即为叶节点的个数，记为 leaf 。则至少在树上添加 (leaf+1)/2 条边，就能使树达到边二连通，所以至少添加的边数就是(leaf+1)/2。
(证明略，请读者感性思考。。。)

双连通分支

在图 G 的所有子图 G’中，如果 G’是双连通的,则称 G’为双连通子图。如果一个双连通子图 G’它不是任何一个双连通子图的真子集,则 G’为极大双连通子图。双连通分支(biconnected component),或重连通分支, 就是图的极大双连通子图。特殊的,点双连通分支又叫做块。

求割点与桥

该算法是 R.Tarjan 发明的。对图深度优先搜索,定义 DFS(u)为 u 在搜索树(以下简称为树)中被遍历到的次序号。定义 Low(u)为 u 或 u 的子树中能通过非父子边追溯到的最早的节点,即 DFS 序号最小的节点。根据定义,则有:Low(u)=Min{DFS(u)DFS(v)(u,v)为后向边(返祖边)等价于 DFS(v) < DFS(u)且 v 不为 u 的父亲节点 Low(v)(u,v)为树枝边(父子边)}一个顶点 u 是割点,当且仅当满足(1)或(2)(1)u 为树根,且 u 有多于一个子树。(2)u 不为树根,且满足存在(u,v)为树枝边(或称父子边,即 u 为 v 在搜索树中的父亲),使得 DFS(u) <= Low(v)。一条无向边(u,v)是桥,当且仅当(u,v)为树枝边,且满足 DFS(u) < Low(v)。

void Tarjan(int u, int father) //father 是u的父节点
{
	Father[u] = father;
	int i,j,k;
	low[u] = dfn[u] = nTime ++;
	for( i = 0;i < G[u].size() ;i ++ ) {
		int v = G[u][i];
		if( ! dfn[v]) {
			Tarjan(v,u);
			low[u] = min(low[u],low[v]);
                        if(low[u]>low[u]) u,v为桥
 }
		else if( father != v ) //连到父节点的回边不考虑，否则求不出桥
			low[u] = min(low[u],dfn[v]);
	}
}
void Count()
{ //计算割点和桥
    int nRootSons = 0;    int i;
    Tarjan(1,0);
    for( i = 2;i <= n;i ++ ) {
        int v = Father[i];
        if( v == 1 )
            nRootSons ++; //DFS树中根节点有几个子树
        else {
            if( dfn[v] <= low[i])
                bIsCutVetext[v] = true;
        }
    }
    if( nRootSons > 1)
        bIsCutVetext[1] = true;
    for( i = 1;i <= n;i ++ )
        if( bIsCutVetext[i] )
            cout << i << endl;
    for( i = 1;i <= n;i ++) {
        int v = Father[i];
        if(v >0 &&  dfn[v] < low[i])
            cout << v << "," << i <<endl;
    }
}

求双连通分支

下面要分开讨论点双连通分支与边双连通分支的求法。
对于点双连通分支,实际上在求割点的过程中就能顺便把每个点双连通分支求出。建立一个栈,存储当前双连通分支,在搜索图时,每找到一条树枝边或后向边(非横叉边),就把这条边加入栈中。如果遇到某时满 足 DFS(u) <= Low(v),说明 u 是一个割点,同时把边从栈顶一个个取出,直到遇到了边(u,v),取出的这些边与其关联的点,组成一个点双连通分支。割点可以属于多个点双连通分支,其余点和每条边只属于且属于一个点双连通分支。对于边双连通分支,求法更为简单。只需在求出所有的桥以后,把桥边删除,原图变成了多个连通块,则每个连通块就是一个边双连通分支。桥不属于任何一个边双连通分支,其余的边和每个顶点都属于且只属于一个边双连通分支。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<map>
using namespace std ;

const int maxn = 5000 + 10 ;
const int maxm = 20000 + 10 ;
struct Edge{
    int to , next ;
    //该边是否为桥
    bool cut ;
}edge[maxm];
int head[maxn] , tot ;

//Low[u]表示u所能追溯到的在栈中最早的节点，该Low数组和求割点与桥的Low数组定义不一样
int Low[maxn] , DFN[maxn] , Stack[maxn] , Belong[maxn] ;
int Index , top ;
//边双连通块数
int block ;
bool Instack[maxn] ;
//桥的数目
int bridge ;

void addedge( int u , int v){
    edge[tot].to = v ;edge[tot].next = head[u] ;edge[tot].cut = false ;
    head[u] = tot ++ ;
}
void Tarjan( int u , int pre){
    int  v ;
    Low[u] = DFN[u] = ++ Index ;
    Stack[top ++] = u ;
    Instack[u] = true ;

    for( int i = head[u] ; i != -1 ;i = edge[i].next ){
        v = edge[i].to ;
        if( v == pre) continue ;
        //树枝边
        if( !DFN[v  ]){
            //回溯从叶子结点开始处理，一直到根节点
            Tarjan( v , u ) ;
            //对于树枝边（u，v)，修改low[u]之前一定有何v相连的回向边修改了 Low[v]，造成v的Low数值变小
            if( Low[u] > Low[v] )
                Low[u] = Low[v] ;
            //桥边，回溯过后v所能追溯到的标号最小的节点依旧比u的编号大，这时Low[v] = DFN[v] ;
            if( Low[v] > DFN[u]){
                bridge ++ ;
                edge[i].cut = true ;
                edge[i ^ 1].cut = true ;
            }
        }
        //（u，v)回向边，修改u所能追溯到的编号最小的节点
        else if( Instack[v] && Low[u] > DFN[v])
            Low[u] = DFN[v] ;
    }
    //u节点是该连通分量的根节点
    if( Low[u] == DFN[u]){
        block ++ ;
        do{
            v = Stack[ -- top ] ;
            Instack[v] = false ;
            Belong[v] = block ;
        }
        while( v != u ) ;
    }
}

void ini(){
    tot = 0 ;
    memset( head , -1 , sizeof( head ) ) ;
}

//缩点后形成树，每个点的度数
int du[maxn] ;
void solve( int n ){
    memset( DFN , 0 ,sizeof( DFN )) ;
    memset( Instack , false , sizeof( Instack )) ;
    Index = top = block = 0 ;
    Tarjan( 1 , 0 ) ;


    int ans = 0 ;
    memset( du , 0 , sizeof( du )) ;
    for(int i = 1 ;i<=n ;i++){
        for(int j = head[i] ;j!=-1 ; j=edge[j].next )
            if( edge[j].cut )
                du[Belong [i]] ++;
    }
    for(int i = 1 ;i<=block ; i++)
        if( du [i] == 1)
            ans ++;
    printf("%d\n" , ( ans + 1) / 2 ) ;
}

int main(){
    int n , m ;
    int u , v ;
    while( scanf("%d%d" , & n , & m ) == 2){
        ini() ;
        while( m -- ){
            scanf("%d%d" , &u , & v ) ;
            addedge( u , v ) ;
            addedge( v , u ) ;
        }
        solve( n ) ;
    }
}

构造双连通图

一个有桥的连通图,如何把它通过加边变成边双连通图?
方法为首先求出所有的桥,然后删除这些桥边, 剩下的每个连通块都是一个双连通子图。把每个双连通子图收缩为一个顶点,再把桥边加回来,最后的这个图一定是一棵树,边连通度为 1。统计出树中度为 1 的节点的个数,即为叶节点的个数,记为 leaf。则至少在树上添加(leaf + 1) / 2 条边,就能使树达到边二连通,所以至少添加的边数就是(leaf + 1) / 2。具体方法为,首先把两个最近公共祖先最远的两个叶节点之间连接一条边,这样可以把这两个点到祖先的路径上所有点收缩到一起,因为一个形成的环一定是双连通的。然后再找两个最近公共祖先最远的两个叶节点,这样一对一对找完,恰好是(leaf + 1) / 2 次,把所有点收缩到了一起。